Dijkstra算法简介
Dijkstra算法算是贪心思想实现的,首先把起点到所有点的距离存下来找个最短的,然后松弛一次再找出最短的,所谓的松弛操作就是,遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近,如果更近了就更新距离,这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。
算法核心
-
选择一个节点标记成已经遍历
-
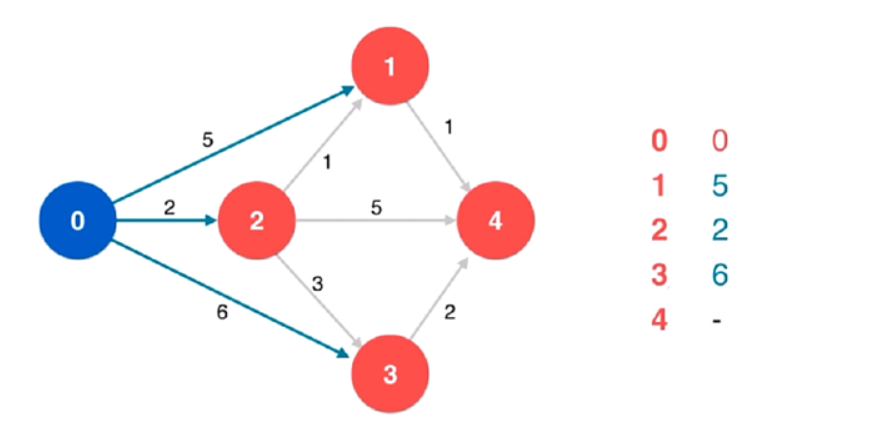
选择从起点到其他节点路径最短的节点,如图所示起始点0到1、2、3的距离分别为5、2、6,当前不可达的4记作无穷大,则下一个被选择的节点就是2
-
-
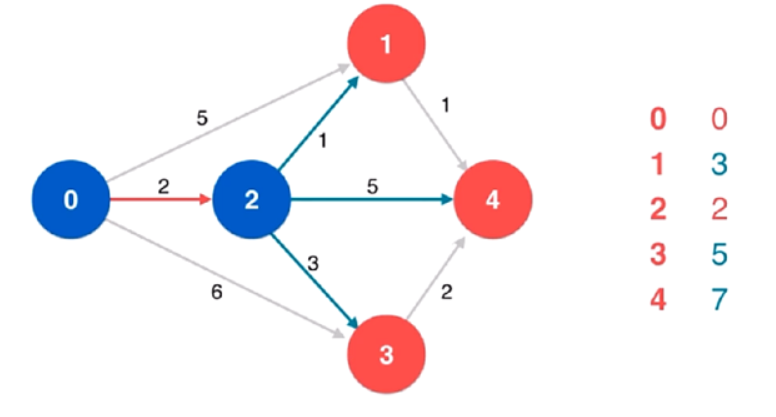
在遍历过程中更新起始点到其他节点的最短距离
-
从起始点0到1的距离为5,按照步骤一选取下个节点2后,0->2->1距离比0->1距离要短(这里已经间接说明为什么第一步要选择2的原因了),需要将距离由5更新为3
-
-
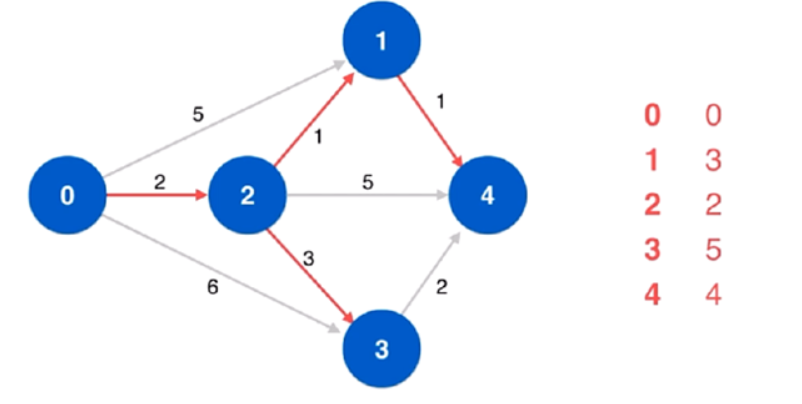
Dijkstra算法终止条件:遍历完毕所有可达的节点
算法实现
LeetCode题目743. 网络延迟时间,这里我直接用优先队列来实现节点的选择,更能说明问题。
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k)
{
vector<int> dis(n + 1, -1);
dis[k] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; // 元素递增
pq.push(make_pair(0, k)); // first:距离, second:节点编号
while (!pq.empty()) {
pair<int, int> dst = pq.top();
pq.pop(); // 选取优先队列中第一个节点,即从起点到其他节点路径最短的节点
if (dst.first > dis[dst.second]) { // 当前达到dst的权值比记录的还要大,则不可能是最短路径
continue;
}
for (int i = 0; i < times.size(); i++) {
if (times[i][0] != dst.second) {
continue;
}
// 遍历以dst为起点的路径
int v = times[i][1];
int w = dst.first + times[i][2];
if (dis[v] == -1 || dis[v] > w) {
dis[v] = w; // 更新距离
pq.push(make_pair(w, v));
}
}
}
int ans = 0;
for (int i = 1; i <= n; i++) {
if (dis[i] == - 1) {
return -1;
}
ans = max(ans, dis[i]);
}
return ans;
}
};